QFlux contains various protocols for performing quantum dynamics simulations with quantum devices. Each submodule contains object implementations for these protocols as demonstrated in a publication, as well as comprehensive tutorial notebooks designed to help users understand, implement and build upon various simulation techniques for studying quantum dynamics using quantum computer frameworks. The tutorial implementations are provided in Python, using Jupyter Notebooks to offer detailed explanations in both markdown and code comments.

QFlux is an open-source Python framework for simulating quantum dynamics in chemical systems across classical and quantum platforms. It unifies wavefunction propagation, Lindblad and generalized quantum master equations, operator splitting, and variational quantum algorithms in a modular, reproducible architecture. Part I presents the theoretical foundations, software design, and scope of QFlux, positioning it as both a research and teaching platform for hybrid classical–quantum simulation. 

Presentation

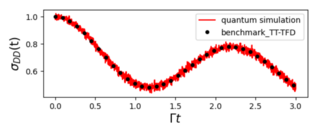
This tutorial introduces practical algorithms for simulating real-time quantum dynamics on qubit-based hardware using QFlux. Molecular and spin Hamiltonians are mapped to Pauli operators and quantum circuits, with observables extracted via measurement or the Hadamard test. New methods include the Quantum Split-Operator Fourier Transform and a variational time-evolution scheme. Benchmarks demonstrate accurate, noise-resilient simulations on near-term devices. 

Presentation

Part III provides an implementation-focused guide to quantum state preparation and unitary synthesis for n-qubit systems in QFlux. It covers recursive multiplexor and uniformly controlled rotation methods for state initialization, and extends them to full unitary decompositions using Givens rotations, cosine–sine, quantum Shannon, and Walsh decompositions. The tutorial links linear-algebraic factorizations to hardware-efficient circuits with explicit gate-count scaling. 

Presentation

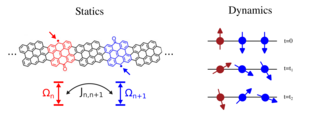
This installment extends QFlux to open quantum systems governed by non-unitary dynamics. Using the Lindblad master equation, it shows how dissipation, decoherence, and environmental effects can be modeled and simulated for spin systems and chemical double-well potentials. The tutorial introduces dilation techniques that embed open-system dynamics into enlarged unitary spaces, enabling execution on quantum hardware and laying groundwork for more advanced treatments. 

Presentation

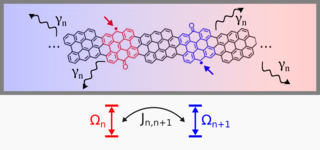
Part V introduces adaptive variational quantum algorithms for simulating open-system dynamics within QFlux. Using the qmad module, the tutorial walks through workflows for solving the Lindblad equation with adaptive ansätze. Applications include the amplitude-damping channel and the Fenna–Matthews–Olson complex. Methods such as unrestricted adaptive variational quantum dynamics and stochastic Schrödinger trajectories provide hands-on insight into dissipative simulations. 

Presentation

This tutorial focuses on non-Markovian open quantum dynamics described by the generalized quantum master equation. Leveraging the Nakajima–Zwanzig formalism and the Sz.-Nagy dilation theorem, QFlux embeds memory-dependent, non-unitary evolution into unitary dynamics suitable for quantum simulation. Using the spin–boson model, the tutorial connects theory to executable workflows for studying finite-temperature and memory-driven quantum processes.

Presentation