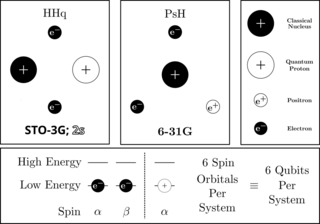
53. Error-Mitigation Enabled Multicomponent Quantum Simulations Beyond the Born-Oppenheimer Approximation
We present a multicomponent unitary coupled cluster framework for quantum simulations that include electronic and nuclear quantum effects beyond Born–Oppenheimer. Using the nuclear-electronic orbital formalism, we build mcUCC ansätze for positronium hydride and H2 with a quantum proton and assess hardware demands. To reduce resources, we apply the local unitary cluster Jastrow ansatz and demonstrate it on IBM Q’s Heron device. With PIE, ground-state energies achieve chemical accuracy, marking the first error-mitigated multicomponent correlated simulation on quantum hardware.
52. FragmentRetro: A Quadratic Retrosynthetic Method Based on Fragmentation Algorithms
Retrosynthesis underpins computer-aided synthesis planning, yet tree-search methods face exponential scaling. We introduce FragmentRetro, a fragmentation-based approach using BRICS/r-BRICS, stock-aware exploration, and fingerprint screening to achieve quadratic complexity. Evaluations on PaRoutes, USPTO-190, and natural products show high solved rates and competitive runtimes, including cases where tree search fails, establishing FragmentRetro as a scalable foundation for automated synthesis planning.

51. Qumode-Based Variational Quantum Eigensolver for Molecular Excited States
We introduce Qumode Subspace VQE (QSS-VQE), a hybrid quantum-classical algorithm for molecular excited states using bosonic qumodes in cQED. By embedding qubit-mapped Hamiltonians into Fock space, QSS-VQE enables efficient state preparation and reduced quantum resources. Simulations of H₂, cytosine, and a bosonic model highlight the expressivity of qumode gates and regimes where qumode-based implementations surpass qubit-only methods, showing promise for advanced quantum molecular simulations.

50. The Quantum Ensemble Variational Optimization Algorithm: Applications to Molecular Inverse Design
Designing molecules with optimized properties is hindered by the combinatorial complexity of molecular structures. We introduce Quantum Ensemble Variational Optimization (QEVO), a method for near-term and early fault-tolerant quantum computing platforms that maps structures to Pauli strings and optimizes a variational ansatz to sample promising candidates. simulations show QEVO can design drug-like anticancer molecules with shallow circuits and few qubits, offering a practical approach to problems of combinatorial complexity.

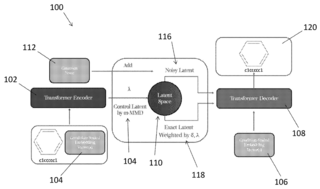
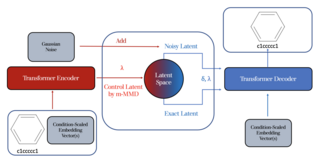
49. Kernel-elastic autoencoder
The present invention relate to a system including a transformer encoder with a compression layer, a transformer decoder with an expansion layer, the transformer encoder configured to transform one or more inputs into a control latent vector, a noise injection element configured to add noise to the control latent vector to create a noisy latent vector, a weighting element configured to add one or more weightings to the control latent vector to create an exact latent vector, and the transformer decoder configured to transform the noisy latent vector and exact latent vector into an output.
48. Holographic Quantum Computing with Compact Quantum Computers
Systems and methods for implementing holographic quantum circuits on compact quantum computing systems are provided. Compact quantum computing systems include systems having fewer physical qubits than the number of quantum modes to be instantiated during execution of the quantum circuit. Techniques described herein may be used to perform boson sampling techniques, including with application to molecular docking simulations.
47. A Hybrid Transformer Architecture with a Quantized Self-Attention Mechanism Applied to Molecular Generation
We propose a hybrid quantum-classical self-attention mechanism within a transformer decoder to enhance efficiency in large language models. Applied to chemistry, our model trains on the QM9 dataset using SMILES strings for conditional generation. The quantum query-key dot product reduces complexity from O(n2d) to O(n2log d). Simulated on NVIDIA’s CUDA-Q, this approach offers a promising direction for quantum-enhanced Natural Language Processing.
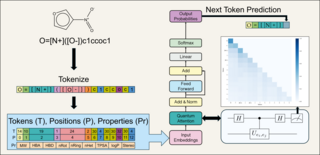
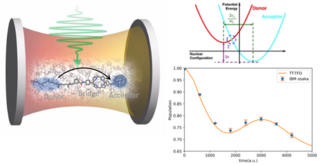
46. A Computational Framework for Simulations of Dissipative Non-Adiabatic Dynamics on Hybrid Oscillator-Qubit Quantum Devices
We present a computational framework for simulating non-adiabatic vibronic dynamics on cQED platforms using hybrid oscillator-qubit hardware with mid-circuit measurements and resets. This approach captures environmental effects like dissipation and dephasing. We simulate energy transfer in a photosynthetic chromophore triad, showing that noise levels below molecular dissipation rates enable accurate simulations for near-term quantum computing applications.
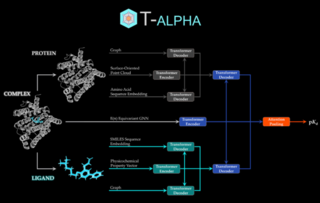
45. T-ALPHA: A Hierarchical Transformer-Based Deep Neural Network for Protein-Ligand Binding Affinity Prediction With Uncertainty-Aware Self-Learning for Protein-Specific Alignment
T-ALPHA is a deep learning model that enhances protein-ligand binding affinity prediction by integrating multimodal features within a hierarchical transformer framework. It outperforms existing models on multiple benchmarks and remains highly accurate even with predicted structures rather than crystal structures. Additionally, it includes an uncertainty-aware self-learning method for protein-specific alignment, improving ranking of ligands for biologically significant targets, such as the SARS-CoV-2 main protease and the epidermal growth factor receptor.
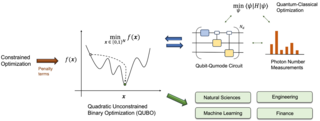
44. Solving Constrained Optimization Problems Using Hybrid Qubit-Qumode Quantum Devices
Optimization challenges span a wide array of fields, from logistics and scheduling to finance, materials science, and drug discovery. We introduce an approach for solving Quadratic Unconstrained Binary Optimization problems using hybrid qubit-qumode bosonic quantum devices. Trial states are prepared through universal qubit-qumode circuits, employing echoed conditional displacement (ECD) gates in combination with qubit rotations. Our approach demonstrates the immense potential of hybrid quantum systems, showcasing their ability to efficiently tackle complex optimization problems in society.
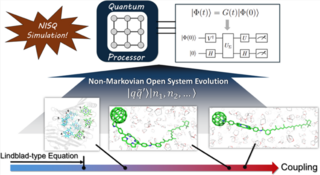
43. Simulating Non-Markovian Quantum Dynamics on NISQ Computers Using the Hierarchical Equations of Motion
In this work, we introduce a quantum algorithm designed to simulate non-Markovian dynamics of open quantum systems. Our approach enables the implementation of arbitrary quantum master equations on noisy intermediate-scale quantum (NISQ) computers. We illustrate the method as applied in conjunction with the numerically exact hierarchical equations of motion (HEOM) method. The effectiveness of the resulting quantum HEOM algorithm (qHEOM) is demonstrated as applied to simulations of the non-Lindbladian electronic energy and charge transfer dynamics in a triad model and the FMO complex.
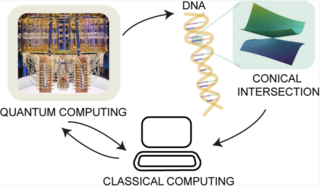
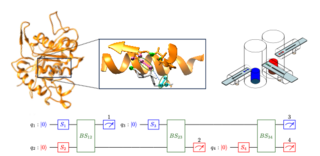
42. Characterizing conical intersections of nucleobases on quantum computers
In this work, we present the first quantum simulation of conical intersections (CIs) in a biomolecule, cytosine, using a superconducting quantum computer. We apply the Contracted Quantum Eigensolver (CQE) – with comparisons to conventional Variational Quantum Deflation (VQD) – to compute the near-degenerate ground and excited states associated with the conical intersection, a key feature governing the photostability of DNA and RNA.
41. Impact of Quantum Mechanics-Based Workshops on Developing High School Students’ Interest and Intuition in Quantum Information Science
In the United States, quantum concepts are introduced at a fragmented level in high schools, and efforts to implement a quantum curriculum at the secondary level have been limited. This presentation describes the development of a workshop, and the associated research to analyze the usage of quantum mechanics-themed games on the development of high school students’ intuition and interest in topics related to quantum phenomena, such as quantum superposition and quantum measurement.

40. Quantum Machine Learning in Drug Discovery: Applications in Academia and Pharmaceutical Industries
The nexus of quantum computing and machine learning - quantum machine learning - offers the potential for significant advancements in chemistry. This review explores the potential of quantum neural networks on gate-based quantum computers within the context of drug discovery. We discuss the theoretical foundations of quantum machine learning, including data encoding, variational quantum circuits, and hybrid quantum-classical approaches. Applications to drug discovery are highlighted.
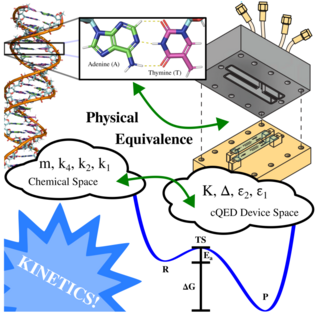
39. A Roadmap for Simulating Chemical Dynamics on a Parametrically Driven Bosonic Quantum Device
In this study, we investigate the feasibility of simulating chemical reaction dynamics using a parametrically driven bosonic superconducting Kerr-cat device. This approach provides control over parameters defining the double-well free energy profile, as well as external factors like temperature and the coupling strength between the reaction coordinate and the thermal bath of non-reactive degrees of freedom. We demonstrate the effectiveness of this protocol for prototypical chemical systems.
38. Oscillatory dissipative tunneling in an asymmetric double-well potential
Dissipative tunneling remains a cornerstone effect in quantum mechanics. In chemistry, it plays a crucial role in governing the rates of chemical reactions, often modeled as the motion along the reaction coordinate from one potential well to another. In this paper, we show that a continuously driven Kerr parametric oscillator with third order non-linearity can be operated in the quantum regime to create a fully tunable asymmetric double-well, which paves the way for analog molecular simulators.
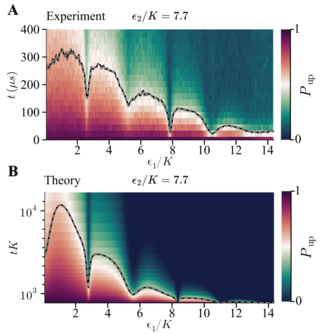
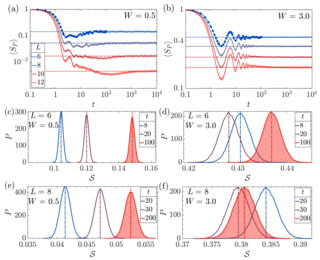
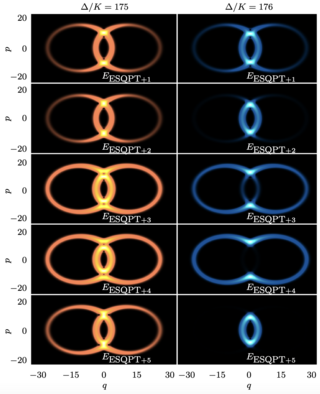
37. Chaos destroys the excited state quantum phase transition of the Kerr parametric oscillator
The driven Kerr parametric oscillator undergoes an excited state quantum phase transition (ESQPT) linked to an unstable classical periodic orbit. This ESQPT manifests as a singularity in level density near the classical separatrix, which divides phase space. Quantum states below this separatrix form cat-like structures resistant to local decoherence, making them useful for quantum technologies. However, chaos from the external drive and system nonlinearities destroys the ESQPT and cat states, highlighting the need for theoretical analysis in designing highly nonlinear parametric oscillators.

36. Quantum computing and chemistry
As the year-to-year gains in speeds of classical computers continue to taper off, computational chemists are increasingly examining quantum computing as a possible route to achieve greater computational performance. Quantum computers, built upon the properties of superposition, interference, and entanglement of quantum bits, offer, in principle, the possibility to outperform classical computers for solving many important classes of problems, including those in the field of chemistry.
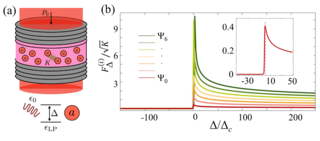
35. Quantum sensing in an exciton-polariton condensate
The extreme sensitivity of critical systems has been explored to improve quantum sensing and weak signal detection. The closing of the energy gap and abrupt change in the nature of the ground state at a quantum phase transition (QPT) critical point enhance indicators of parameter estimation, such as the quantum Fischer information. Here, we show that even if the system lacks a QPT, the quantum Fischer information can still be amplified due to the presence of an excited-state QPT.
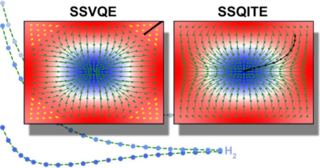
34. Subspace-Search Quantum Imaginary Time Evolution for Excited State Computations
Quantum systems in excited states are attracting significant interest with the advent of noisy intermediate scale quantum (NISQ) devices. While ground states of small molecular systems are typically explored using hybrid variational algorithms like the variational quantum eigensolver (VQE), the study of excited states has received much less attention, partly due to the absence of efficient algorithms. In this work, we introduce the subspace search quantum imaginary time evolution (SSQITE) method
33. Benchmarking various nonadiabatic semiclassical mapping dynamics methods with tensor-train thermo-field dynamics
Accurate quantum dynamics simulations of nonadiabatic processes are important for studies of electron transfer, energy transfer, and pho-
tochemical reactions in complex systems. In this comparative study, we benchmark various approximate nonadiabatic dynamics methods
with mapping variables against numerically exact calculations based on the tensor-train (TT) representation of high-dimensional arrays,
including TT-KSL for zero-temperature dynamics and TT-thermofield dynamics for finite-temperature.
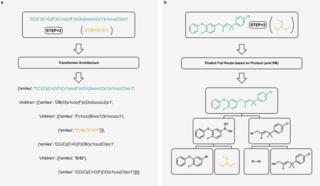
32. DirectMultiStep: Direct Route Generation for Multi-Step Retrosynthesis
Traditional computer-aided synthesis planning (CASP) methods rely on iterative single-step predictions, leading to exponential search space growth that limits efficiency and scalability. We introduce a transformer-based model that directly generates multi-step synthetic routes as a single string by conditionally predicting each molecule based on all preceding ones. The model accommodates specific conditions such as the desired number of steps and starting materials, outperforming …
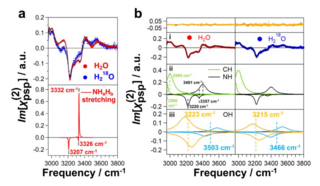
31. Beyond the “Spine of Hydration”: Chiral SFG Spectroscopy Detects DNA First Hydration Shell and Base Pair Structures
Experimental methods capable of selectively probing water at the DNA minor groove, major groove, and phosphate backbone are crucial for understanding how hydration influences DNA structure and function. Chiral-selective sum frequency generation spectroscopy (chiral SFG) is unique among vibrational spectroscopies because it can selectively probe water molecules that form chiral hydration structures around biomolecules. However, interpreting chiral SFG spectra is challenging since both water …
30. Site-Specific Template Generative Approach for Retrosynthetic Planning
We introduce generative machine learning methods for retrosynthetic planning that generate reaction templates. We demonstrate the methodology to design a synthetic pathway for a simple, yet challenging, small molecule of pharmaceutical interest. The pathway was experimentally proven viable through a 3-step process, which compares favorably to previous 5-9 step approaches. Thus, we demonstrate the utility and robustness of the generative machine learning approaches for synthetic chemistry.

29. Simulating electronic structure on bosonic quantum computers
Computations with quantum harmonic oscillators or qumodes is a promising and rapidly evolving approach towards quantum computing. In contrast to qubits, which are two-level quantum systems, bosonic qumodes can in principle have infinite discrete levels, and can also be represented with continuous variable bases. One of the most promising applications of quantum computing is simulating many-fermion problems such as molecular electronic structure…
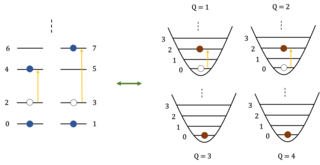
28. Simulating Chemistry on Bosonic Quantum Devices
Bosonic quantum devices offer a novel approach to realize quantum computations, where the quantum two-level system (qubit) is replaced with the quantum (an)harmonic oscillator (qumode) as the fundamental building block of the quantum simulator. The simulation of chemical structure and dynamics can then be achieved by representing or mapping the system Hamiltonians in terms of bosonic operators. In this perspective, we review recent progress and future potential of using bosonic quantum devices.
27. Simulating Cavity-Modified Electron Transfer Dynamics on NISQ Computers
We present a quantum algorithm based on Tensor-Train Thermo-Field Dynamics to simulate the open quantum dynamics of intramolecular charge transfer modulated by an optical cavity on noisy intermediate-scale quantum (NISQ) computers. We apply our methodology to a model that describes intermolecular charge transfer within the carotenoid-porphyrin-C60 molecular triad solvated in tetrahydrofuran (THF within an optical cavity. We find how the dynamics is influenced by the cavity resonance frequency…
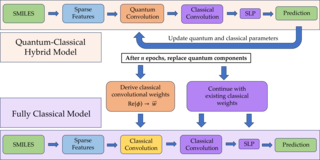
26. Quantum to Classical Neural Network Transfer Learning Applied to Drug Toxicity Prediction
Toxicity is a roadblock that prevents an inordinate number of drugs from being used in potentially life-saving applications. We present a hybrid quantum-classical neural network (QCNN) for predicting drug toxicity, using a quantum circuit design that mimics CNN by explicitly calculating matrix products with complexity O(n2). We believe combining the quantum advantage of reduced complexity and the classical noise-free calculation will pave the way to more scalable machine learning models.
25. Holographic Gaussian Boson Sampling with Matrix Product States on 3D cQED Processors
We introduce quantum circuits for simulations of multi-mode state-vectors on 3D cQED processors, using matrix product states. The circuits are applied to simulations of molecular docking based on holographic Gaussian boson sampling, as illustrated for binding of a thiol-containing aryl sulfonamide ligand to the tumor necrosis factor-α converting enzyme receptor. We show that cQED devices with a modest number of modes could be employed to simulate multimode systems…
24. CardioGenAI: A Machine Learning-Based Framework for Re-Engineering Drugs for Reduced hERG Liability
Drug-induced cardiotoxicity is a major health concern which can lead to serious adverse effects including life-threatening cardiac arrhythmias. It is therefore of tremendous ,interest to develop methods to identify hERG-active compounds, as well as to optimize commercially available drugs for reduced hERG activity. In this work, we present CardioGenAI, a machine learning-based framework for re-engineering drugs for reduced hERG activity while preserving their pharmacolological properties.
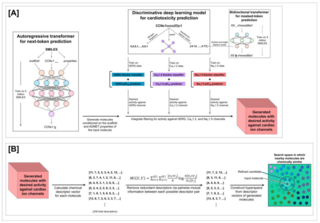
23. Kernel-Elastic Autoencoder for Molecular Design
We introduce the Kernel-Elastic Autoencoder (KAE), a self-supervised generative model based on the transformer architecture with enhanced performance for molecular design. KAE has demonstrated its capability to generate molecules with favorable binding affinities in docking applications, as evidenced by AutoDock Vina and Glide scores, outperforming all existing candidates from the training dataset. Moreover, KAE holds promise to solve problems by generation across a broad spectrum of application
22. Designing variational ansatz for quantum-enabled simulation of non-unitary dynamical evolution - an excursion into Dicke super-radiance
In this study, we employ the Adaptive Variational Quantum Dynamics Algorithm to simulate and benchmark various non-unitarily evolving systems. We exemplify how construction of an expressible ansatz unitary and the associated operator pool can be implemented to analyze examples such as the FMO complex and even the permutational invariant Dicke model of quantum optics.
21. Proposal for Many-body Quantum Chaos Detection
In this work, we use the term “quantum chaos” to refer to spectral correlations similar to those found in random matrix theory. Quantum chaos can be diagnosed through the analysis of level statistics using the spectral form factor, which detects both short- and long-range level correlations.
20. Effective versus Floquet Theory for the Kerr Parametric Oscillator
Parametric gates and processes engineered from the perspective of the static effective Hamiltonian of a driven system are central to quantum technology. However, the perturbative expansions used to derive static effective models may not be able to efficiently capture all the relevant physics of the original system. In this work, we investigate the conditions for the validity of the usual low-order static effective Hamiltonian used to describe a Kerr oscillator under a squeezing drive.
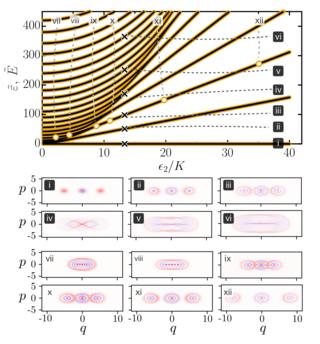
19. Quantum Computing for Chemistry
Quantum computing is an emerging technology with the potential to revolutionize computational studies in chemistry and materials science. Unlike conventional classical computers, quantum computers can harness the power of quantum superpositions and entangled states to achieve a quantum advantage in various challenging computational chemistry problems. In recent years, there has been a growing interest in exploring new ways to apply quantum computing to chemistry.

18. Driving Superconducting Qubits into Chaos
Kerr parametric oscillators are potential building blocks for fault-tolerant quantum computers. They can stabilize Kerr-cat qubits, which offer advantages towards the encoding and manipulation of error-protected quantum information. Kerr-cat qubits have been recently realized with the SNAIL transmon superconducting circuit by combining nonlinearities and a squeezing drive. These superconducting qubits can lead to fast gate times due to their access to large anharmonicities.
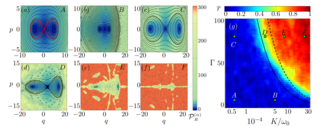
17. A Diagrammatic Method to Compute the Effective Hamiltonian of Driven Nonlinear Oscillators
In this work, we present a new method, based on Feynman-like diagrams, for computing the effective Hamiltonian of driven nonlinear oscillators. The pictorial structure associated with each diagram corresponds directly to a Hamiltonian term, the prefactor of which involves a simple counting of topologically equivalent diagrams. We also leverage the algorithmic simplicity of our scheme in a readily available computer program that generates the effective Hamiltonian to arbitrary order.
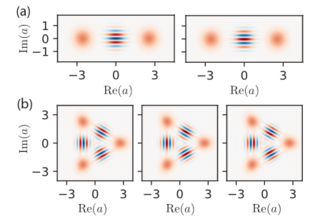
16. A Driven Quantum Superconducting Circuit with Multiple Tunable Degeneracies
We present the experimental discovery of multiple simultaneous degeneracies in the spectrum of a Kerr oscillator subjected to a squeezing drive. This squeezing, in combination with the Kerr interaction creates an effective static two-well potential in the frame rotating at half the frequency of the sinusoidal driving force. Remarkably, these degeneracies can be turned on-and-off on demand, and their number is tunable.
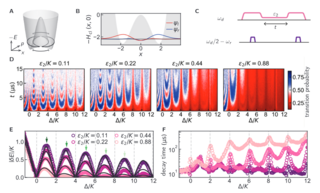
15. Symmetries of the Squeeze-driven Kerr Oscillator
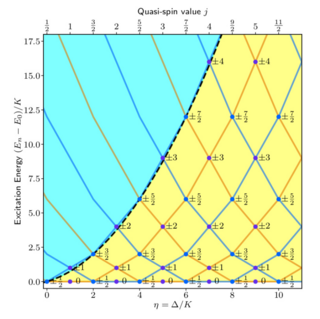
We study the symmetries of the static effective Hamiltonian of a driven superconducting nonlinear oscillator, the so-called squeeze-driven Kerr Hamiltonian, and discover a remarkable quasi-spin symmetry su(2) at integer values of the ratio η = ∆/K of the detuning parameter ∆ to the Kerr coefficient K. We investigate the stability of this newly discovered symmetry to high-order perturbations arising from the static effective expansion of the driven Hamiltonian.
14. Boosting Quantum Amplitude Exponentially in Variational Quantum Algorithms
We introduce a family of variational quantum algorithms, which we coin as quantum iterative power algorithms (QIPAs), and demonstrate their capabilities as applied to global-optimization numerical experiments. Specifically, we demonstrate the QIPA based on a double exponential oracle as applied to ground state optimization of the H2 molecule, search for the transmon qubit ground-state, and biprime factorization.
13. Quantum Multifractality as a Probe of Phase Space in the Dicke Model
We study the multifractal behavior of coherent states projected in the energy eigenbasis of the spin-boson Dicke Hamiltonian, a paradigmatic model describing the collective interaction between a single bosonic mode and a set of two-level systems. By examining the linear approximation and parabolic correction to the mass exponents, we find ergodic and multifractal coherent states and show that they reflect details of the structure of the classical phase space, including chaos, and regularity.
12. The Landscape of Computational Approaches for Artificial Photosynthesis
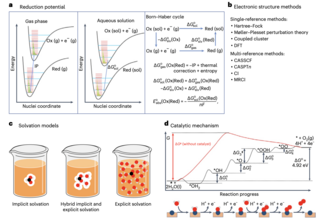
Artifcial photosynthesis is an attractive strategy for converting solar energy into fuels, largely because the Earth receives enough solar energy in one hour to meet humanity’s energy needs for an entire year. However, developing devices for artifcial photosynthesis remains difcult and requires computational approaches to guide and assist the interpretation of experiments.
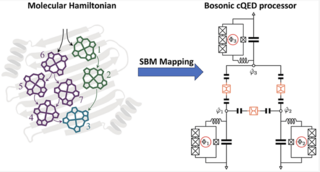
11. Mapping Molecular Hamiltonians into Hamiltonians of Modular cQED Processors
We introduce a general method based on the operators of the Dyson-Masleev transformation to map the Hamiltonian of an arbitrary model system into the Hamiltonian of a circuit Quantum Electrodynamics (cQED) processor. Furthermore, we introduce a modular approach to programming a cQED processor with components corresponding to the mapping Hamiltonian
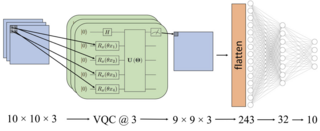
10. Quantum Convolutional Neural Networks for Multi-Channel Supervised Learning
As the rapidly evolving field of machine learning continues to produce incredibly useful tools and models, the potential for quantum computing to provide speed up for machine learning algorithms is becoming increasingly desirable. In particular, quantum circuits in place of classical convolutional filters for image detection-based tasks are being investigated for the ability to exploit quantum advantage.
9. Quantum Tunneling and Level Crossings in the Squeeze-driven Kerr Oscillator
The quasienergy spectrum recently measured in experiments with a squeeze-driven superconducting Kerr oscillator showed good agreement with the energy spectrum of its corresponding static effective Hamiltonian. The experiments also demonstrated that the dynamics of low-energy states can be explained with the same emergent static effective model.
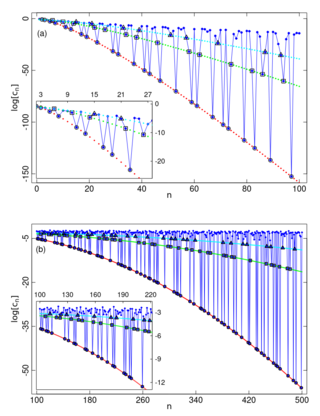
8. Identifying Primes from Entanglement Dynamics
The distribution of primes over the set of natural numbers is a fascinating subject closely related to topics that range from the fundamental problem of factorization to applications in cryptography. Despite numerous efforts, efficient methods to locate huge primes are still under investigation. Here, we present an alternative approach to identifying prime numbers that is based on the evolution of the linear entanglement entropy.
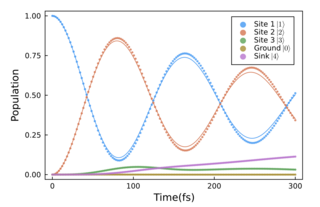
7. Quantum Simulation of the Radical Pair Dynamics of the Avian Compass
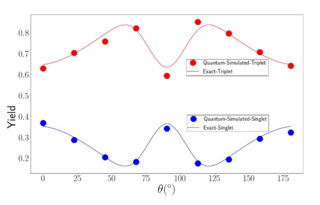
The simulation of open quantum dynamics on quantum circuits has attracted wide interests recently with a variety of quantum algorithms developed and demonstrated. Among these, one particular design of a unitarydilation-based quantum algorithm is capable of simulating general and complex physical systems. In this paper, we apply this quantum algorithm to simulating the dynamics of the radical pair mechanism in the avian compass.
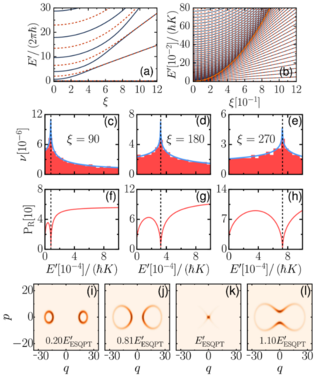
6. Spectral Kissing and its Dynamical Consequences in the Squeezed Kerr-nonlinear Oscillator
Transmon qubits are the predominant element in circuit-based quantum information processing, such as existing quantum computers, due to their controllability and ease of engineering implementation. But more than qubits, transmons are multilevel nonlinear oscillators that can be used to investigate fundamental physics questions. Here, they are explored as simulators of excited state quantum phase transitions (ESQPTs), which are generalizations of quantum phase transitions to excited states.
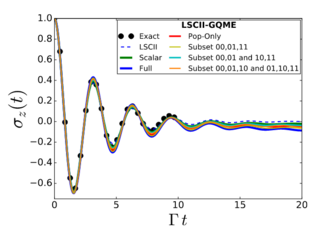
5. Simulating Open Quantum System Dynamics on NISQ Computers with Generalized Quantum Master Equations
We present a quantum algorithm based on the generalized quantum master equation (GQME) approach to simulate open quantum system dynamics on noisy intermediate scale quantum (NISQ) computers. This approach overcomes the limitations of the Lindblad equation, which assumes weak system− bath coupling and Markovity, by providing a rigorous derivation of the equations of motion for any subset of elements of the reduced density matrix.
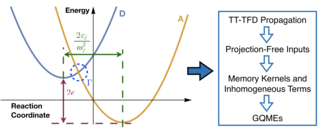
4. Tensor-Train Thermo-Field Memory Kernels for Generalized Quantum Master Equations
In the context of electronic dynamics, the memory kernel and inhomogeneous term of the GQME introduce the implicit coupling to nuclear motion and dynamics of electronic density matrix elements that are projected out (e.g., the off-diagonal elements), allowing for efficient quantum dynamics simulations. Here, we focus on benchmark quantum simulations of electronic dynamics in a spin-boson model system described by various types of GQMEs.
3. Observation of Pairwise Level Degeneracies and the Quantum Regime of the Arrhenius Law in a Double-Well Parametric Oscillator
By applying a microwave drive to a specially designed Josephson circuit, we have realized an elementary quantum optics model, the squeezed Kerr oscillator. This model displays, as the squeezing amplitude is increased, a cross-over from a single ground state regime to a doubly-degenerate ground state regime. In the latter case, the ground state manifold is spanned by Schr¨odinger-cat states, i.e. quantum superpositions of coherent states with opposite phases.
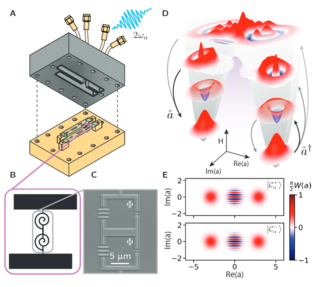
2. Walking with the Atoms in a Chemical Bond : A Perspective using Quantum Phase Transition
Classical phase transitions, like solid-liquid-gas or order-disorder spin magnetic phases, are all driven by thermal energy fluctuations by varying the temperature. On the other hand, quantum phase transitions happen at absolute zero temperature with quantum fluctuations causing the ground state energy to show abrupt changes as one varies the system parameters like electron density, pressure, disorder, or external magnetic field.
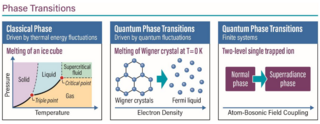
1. Simulating the Dynamics of Electronic Observables via Reduced-dimensionality Generalized Quantum Master Equations
We describe a general-purpose framework for formulating the dynamics of any subset of electronic reduced density matrix elements in terms of a formally exact generalized quantum master equation (GQME). Within this framework, the effect of coupling to the nuclear degrees of freedom, as well as to any projected-out electronic reduced density matrix elements, is captured by a memory kernel and an inhomogeneous term, whose dimensionalities are dictated by the number of electronic reduced density…
Earlier Publications by the PIs and Collaborators
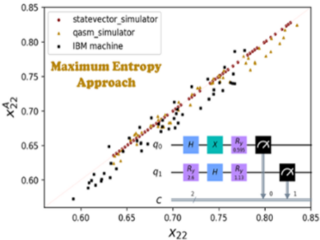
Maximal Entropy Approach for Quantum State Tomography
Quantum computation has been growing rapidly in both theory and experiments. In particular, quantum computing devices with a large number of qubits have been developed by IBM, Google, IonQ, and others. The current quantum computing devices are noisy intermediate-scale quantum devices, and so approaches to validate quantum processing on these quantum devices are needed.
Experimental Detection of the Correlation Rényi Entropy in the Central Spin Model
We propose and experimentally measure an entropy that quantifies the volume of correlations among qubits. The experiment is carried out on a nearly isolated quantum system composed of a central spin coupled and initially uncorrelated with 15 other spins. Because of the spin-spin interactions, information flows from the central spin to the surrounding ones forming clusters of multispin correlations that grow in time.
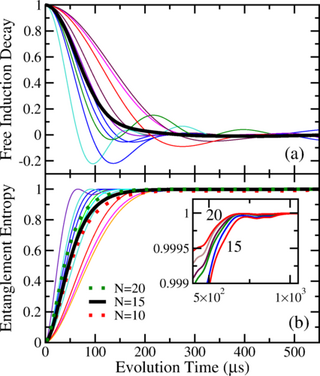
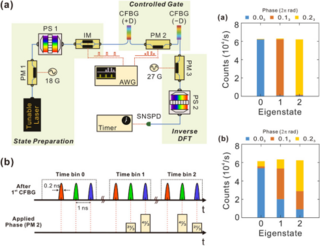
Quantum Phase Estimation with Time-Frequency Qudits in a Single Photon
Quantum computation has received enormous attention in recent years with rapid progress in both theoretical and experimental fronts. The development of quantum algorithms used for quantum computation has been stimulated by the greater availability of more capable quantum devices. The phase estimation algorithm (PEA) is a key subroutine of several important algorithms such as the Shor’s factorization algorithm and the Harrow–Hassidim–Lloyd (HHL)algorithm for solving linear systems of equations.
Qudits and High-Dimensional Quantum Computing
Qudit is a multi-level computational unit alternative to the conventional 2-level qubit. Compared to qubit, qudit provides a larger state space to store and process information, and thus can provide reduction of the circuit complexity, simplification of the experimental setup and enhancement of the algorithm efficiency. This review provides an overview of qudit-based quantum computing covering a variety of topics ranging from circuit building, algorithm design, to experimental methods.
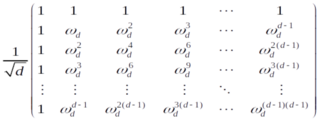
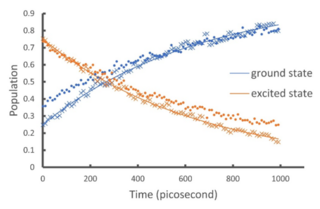
A Quantum Algorithm for Evolving Open Quantum Dynamics on Quantum Computing Devices
Qudit is a multi-level computational unit alternative to the conventional 2-level qubit. Compared to qubit, qudit provides a larger state space to store and process information, and thus can provide reduction of the circuit complexity, simplification of the experimental setup and enhancement of the algorithm efficiency. This review provides an overview of qudit-based quantum computing covering a variety of topics ranging from circuit building, algorithm design, to experimental methods.
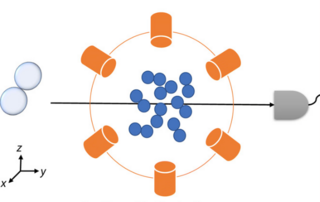
Efficient Multiphoton Sampling of Molecular Vibronic Spectra on a Superconducting Bosonic Processor
The efficient simulation of quantum systems is a primary motivating factor for developing controllable quantum machines. For addressing systems with underlying bosonic structures, it is advantageous to utilize a naturally bosonic platform. Optical photons passing through linear networks may be configured to perform quantum simulation tasks, but the efficient preparation and detection of multiphoton quantum states of light in linear optical systems are challenging.
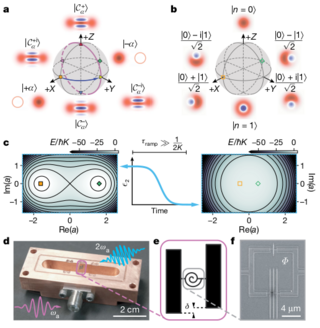
Stabilization and Operation of a Kerr-cat Qubit
Quantum superpositions of macroscopically distinct classical states—so-called Schrödinger cat states—are a resource for quantum metrology, quantum communication and quantum computation. In particular, the superpositions of two opposite-phase coherent states in an oscillator encode a qubit protected against phase-flip errors1,2. However, several challenges have to be overcome for this concept to become a practical way to encode and manipulate error-protected quantum information.
Entanglement Classifier in Chemical Reactions
The Einstein, Podolsky, and Rosen (EPR) entanglement, which features the essential difference between classical andquantum physics, has received wide theoretical and experimental attentions. Recently, the desire to understand andcreate quantum entanglement between particles such as spins, photons, atoms, and molecules is fueled by the de-velopment of quantum teleportation, quantum communication, quantum cryptography,and quantum computation.
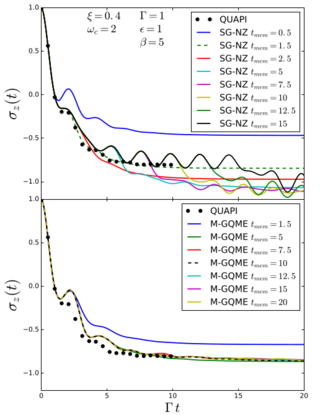
A Modified Approach for Simulating Electronically Nonadiabatic Dynamics via the Generalized Quantum Master Equation
We present a modified approach for simulating electronically nonadiabatic dynamics based on the Nakajima-Zwanzig generalized quantum master equation (GQME). The modified approach utilizes the fact that the Nakajima-Zwanzig formalism does not require casting the overall Hamiltonian in system-bath form, which is arguably neither natural nor convenient in the case of the Hamiltonian that governs nonadiabatic dynamics.
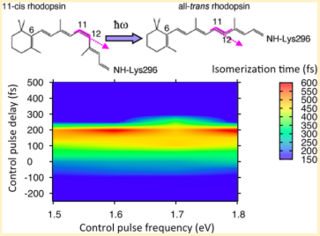
Floquet Study of Quantum Control of the Cis–Trans Photoisomerization of Rhodopsin
Understanding how to control reaction dynamics of polyatomic systems by using ultrafast laser technology is a fundamental challenge of great technological interest. Here, we report a Floquet theoretical study of the effect of light-induced potentials on the ultrafast cis−trans photoisomerization dynamics of rhodopsin.
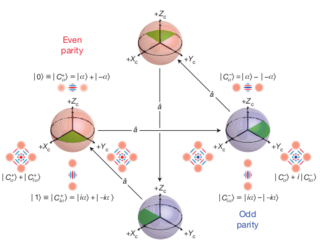
Extending the Lifetime of a Quantum Bit with Error Correction in Superconducting Circuits
Quantum error correction (QEC) can overcome the errors experienced by qubits and is therefore an essential component of a future quantum computer. To implement QEC, a qubit is redundantly encoded in a higher-dimensional space using quantum states with carefully tailored symmetry properties. Projective measurements of these parity-type observables provide error syndrome information, with which errors can be corrected via simple operations.
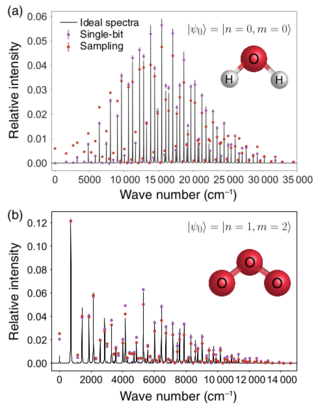
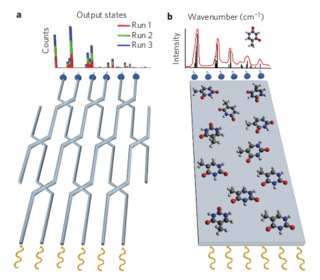
Boson Sampling for Molecular Vibronic Spectra
Controllable quantum devices open novel directions to both quantum computation and quantum simulation. Recently, a problem known as boson sampling has been shown to provide a pathway for solving a computationally intractable problem without the need for a full quantum computer, instead using a linear optics quantum set-up. In this work, we propose a modification of boson sampling for the purpose of quantum simulation.
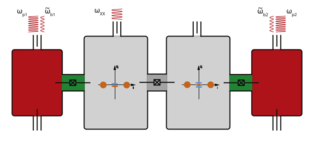
Dynamically Protected Cat-qubits: A New Paradigm for Universal Quantum Computation
We present a new hardware-efficient paradigm for universal quantum computation which is based on encoding, protecting and manipulating quantum information in a quantum harmonic oscillator. This proposal exploits multiphoton driven dissipative processes to encode quantum information in logical bases composed of Schrödinger cat states. More precisely, we consider two schemes.
A Variational Eigenvalue Solver on a Photonic Quantum Processor
Quantum computers promise to efficiently solve important problems that are intractable on a conventional computer. For quantum systems, where the physical dimension grows exponentially, finding the eigenvalues of certain operators is one such intractable problem and remains a fundamental challenge. The quantum phase estimation algorithm efficiently finds the eigenvalue of a given eigenvector but requires fully coherent evolution.

Superconducting Circuits for Quantum Information: An Outlook
The performance of superconducting qubits has improved by several orders of magnitude in the past decade. These circuits benefit from the robustness of superconductivity and the Josephson effect, and at present they have not encountered any hard physical limits. However, building an error-corrected information processor with many such qubits will require solving specific architecture problems that constitute a new field of research.
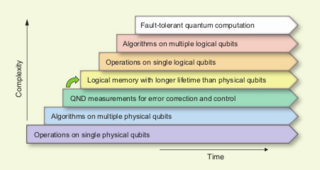
Measuring the Decoherence of a Quantronium Qubit with the Cavity Bifurcation Amplifier
Dispersive readouts for superconducting qubits have the advantage of speed and minimal invasiveness. We have developed such an amplifier, the cavity bifurcation amplifier (CBA), and applied it to the readout of the quantronium qubit. It consists of a Josephson junction embedded in a microwave on-chip resonator.
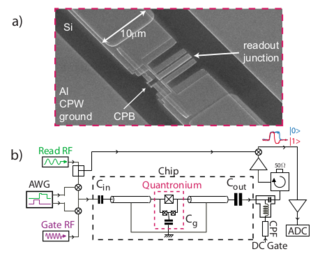
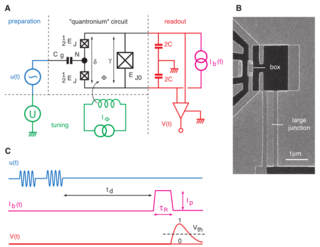
Manipulating the Quantum State of an Electrical Circuit
We have designed and operated a superconducting tunnel junction circuit that behaves as a two-level atom: the “quantronium.” An arbitrary evolution of its quantum state can be programmed with a series of microwave pulses, and a projective measurement of the state can be performed by a pulsed readout subcircuit. The measured quality factor of quantum coherenceQ ϕ ≅ 25,000 is sufficiently high that a solid-state quantum processor based on this type of circuit can be envisioned.